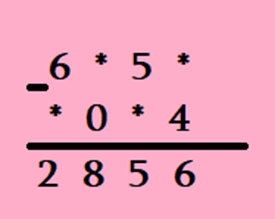Պարապմունք 17

Բնական թվերի գումարման հաշվեկանոնը

Դասարանական առաջադրանքներ

Տնային առաջադրանքներ

1․ Կատարե՛ք գումարում

Օրինակ՝ 6458+2141=8599

			+	6	4	5	8
				2	1	4	1
				8	5	9	9

3249+9815=13064

			+	3	2	4	9
				9	8	1	5
			1	3	0	6	4

93725+698911=792636

		+			9	3	7	2	5
				6	9	8	9	1	1
				7	9	2	6	3	6

65417+41136=106553

			+	6	5	4	1	7
				4	1	1	3	6
			1	0	6	5	5	3

2328+807=3135

			+	2	3	2	8
					8	0	7
				3	1	3	5

2․  Աստղանիշները փոխարինե՛ք այն թվանշաններով, որոնց դեպքում կատարված գումարումը ճիշտ կլինի․

+	6	8	1	4
	4	4	6	7
1	0	2	7	1

+		7	0	3	2	7
		2	0	9	7	3
		8	1	2	0	0

+		4	7	6	3
		9	9	9	9
	1	3	7	5	2

3․ Որո՞նք են այն ամենամեծ և ամենափոքր վեցանիշ թվերը, որոնք կարելի է գրի առնել՝ մեկական անգամ գործածելով 2, 7, 1, 0, 3, 5 թվանշանները։ 753210  102357

4․ Պահեստում կար 7200 աման ներկ, որոնցից խանութները տարան 5400 աման։ Քանի՞ անգամ փոքրացավ պահեստում եղած ներկի ամանների քանակը։7200-5400=1800  7200:1800=4  Պատ.՝4 անգամ

5. Բանավոր հարցեր․

Ո՞րն է բնական թվերի գումարման տեղափոխական հատկությունը։

Ո՞րն է բնական թվերի բազմապատկման տեղափոխական հատկությունը։

Ո՞րն է բնական թվերի գումարման զուգորդական օրենքը։

Ո՞րն է բնական թվերի բազմապատկման զուգորդական օրենքը։

Ո՞րն է բնական թվերի բազմապատկման բաշխական օրենքը գումարման նկատմամբ։

Տնային առաջադրանքներ

1․ Կատարե՛ք գումարում

5992+3779

		+		5	9	9	2
				3	7	7	9
				9	7	7	1

3207+8034=11241

		+		3	2	0	7
				8	0	3	4
			1	1	2	4	1

23051+4158=27209

		+		2	3	0	5	1
					4	1	5	8
				2	7	2	0	9

77528+19056=96584

		+		7	7	5	2	8
				1	9	0	5	6
				9	6	5	8	4

2․  Աստղանիշները փոխարինե՛ք այն թվանշաններով, որոնց դեպքում կատարված գումարումը ճիշտ կլինի․

+	5	5
	3	1
	8	6

+	3	3	7
	4	2	2
	7	5	9

3. Աղջիկն ամեն օր կարդում է 30 էջ, որից հետո էջանշան է դնում գրքի մեջ։ Երբ նա էջանշանը գրքի մեջ դրել է 6 անգամ, նրան մնացել է կարդալու 18 էջ։ Քանի՞ էջ կա գրքում։ 30×6=180  180+18=198 Պատ.`198 էջ

 Բազմապատկման բաշխական օրենքը գումարման նկատմամբ

 Որևէ թիվ երկու թվերի գումարով բազմապատկելու արդյունքը կարելի է ստանալ՝ թիվը բազմապատկելով յուրաքանչյուր գումարելիով և ստացված թվերը գումարելով իրար։

Օրինակ՝ 19‧(7+8)=19‧7+19‧8=133+152=285

Օրինակ՝ 194‧40+194‧60=194‧(40+60)=194‧100=19400

Դասարանական առաջադրանքներ

1․ Հաշվեք արտահայտության արժեքը կիրառելով բաշխական օրեքը․

• 8‧(7+5)=8×7+8×5=96
• 4‧(91+64)=4×91+4×64=364+256=620
• (375+58) ‧2=2×375+2×58=750+116=866
• (119+32) ‧100= 100×119+100×32=11900+3200=15100

2. Օգտագործելով բաշխական օրնեքը ՝ հաշվե՛ք առավել հարմար եղանակով․

Օրինակներ՝

194‧40+194‧60=194‧(40+60)=194‧100=19400

164‧80-164‧30=164‧(80-30)=164‧50=8200

• 132×70+70×68 =70x(132+68)=14000
• 973‧37-27‧37=37x(973-27)=37×946=35002
• 388‧99+12‧99=99x(388+12)=99×400=39600
• 462·120-462·70=462x(120-70)=462×50= 23100

3. Հաշվե՛ք    առավել   հարմար եղանակով․

Օրինակներ՝

194‧40+194‧50+194‧10=194‧(40+50+10)=194‧100=19400

164‧80-164‧20-164‧10=164‧(80-20-10)=164‧50=8200

• 251·256+251·122+251·34=251x(256+122+34)=251×412 =103412
• 361·145+361·53+361·52 =361x(53+52+145)=250×361=9025
• 164·243-164·53-164·9=164x(243-53-9)=181×164=29780

4. Մարդատար գնացքը կազմված է 16 վագոնից, որորնցից յուրաքանչյուրում կա 56 տեղ։ Քանի՞ ազատ տեղ է մնացել, եթե գնացք է նստել 837 ուղևոր։ 16×56=866   866-837=29, պատ.՝ 29տեղ:

5․ Առաջին գրքում կա 256 էջ, երկրորդում՝ 80 էջով ավելի, իսկ երրորդում՝ երկրորդից 112 էջով ավելի։ Քանի՞ էջ կա երրորդ գրքում։

256+80+112=448 պատ.՝ 448էջ

Տնային առաջադրանքներ

1.Հաշվեք արտահայտության արժեքը կիրառելով բաշխական օրնեքը․

• 6‧(9+6)= 6×9+6×6=54+36=90
• (37+5)‧20= 20×37+20×5=740+100=840
• (10-3)‧11= 11×10-11×3=33+110=143
• (11-9)‧12= 12×11+12×9=132+108=240

2.  Հաշվե՛ք    առավել   հարմար եղանակով․

• 7‧3+7‧5+7‧2=7x(3+5+2)=70
• 4‧9+4‧11+4‧3=4x(9+11)+4×3=80+12=92
• 25‧2+25‧3+25‧5=25x(2+3+5)=25×10=250
• 32‧16+32‧4+32‧5

3.  Եթե թիվը գումարենք ինքն իրեն և ավելացնենք 15, կստանանք 137։ Ո՞րն է այդ թիվը։   

137-15=122    122:2=61, պատ.՝ 61

Բազմապատկման տեղափոխական օրենքը՝

Արտադրիչների տեղերը փոխելիս արտադրյալը չի փոխվում։

Օրինակ՝

87‧33=33‧87=2871

Բազմապատկման զուգորդական օրենքը՝

Երկու թվերի արտադրյալը երրորդ թվով բազմապատկելու արդյունքը կարելի է ստանալ՝ առաջին թիվը երկրորդ և երրորդ թվերի արտադրյալով բազմապատկելով։

Օրինակ՝

(27‧5)‧6=27‧(5 ‧6)=810

Դասարանական առաջադրանքներ

1․ Ստուգե՛ք հավասարությունը՝ կատարելով բազմապատկումը։ (բազմապատկումը կատարի՛ր paint ծրագրում)

• 87∙9=9∙87=783
• 25∙33=33∙25=825
• 192∙16=16∙192=3072
• 24∙543=543∙24 =13032

2․ Ստուգե՛ք հավասարությունը:

 (բազմապատկումը կատարի՛ր paint ծրագրում)

• (8∙3) ∙5=8∙(3∙5)=120
• (2∙18) ∙4=2∙(18∙4)=144
• 11∙(8∙9)=(11∙8) ∙9=792
• 27∙(5∙6)=(27∙5) ∙6=810

3. Կիրառելով բազմապատկման զուգորդական օրենքը հաշվել առավել հարմար եղանակով:

• 3∙4∙5=(3×5)x4=60
• 25∙4∙7=700
• 20∙10∙17=3400
• 38∙24∙5=38×120=4560

4. Կիրառելով բազմապատկման տեղափոխական և զուգորդական օրենքները հաշվել առավել հարմար եղանակով:

4∙25∙138=13800

2∙14∙25∙5=2x5x25x14=3500

6∙4∙5∙20=2400

5. Հաշվե՛ք գումարը՝ գումարումը փոխարինելով բազմապատկումով՝

• 290+290+290+290+290+290+290+290+290 =290×9=2610
• 2388+2388+2388=2388×3=7164

6. Գործվածքի՝ 36մ երկարություն ունեցող կտորից կարել են 12միանման թիկնոց։ Քանի՞ մետրգործվածք է անհրաժեշտ 15 այդպիսի թիկնոց կարելու համար։ 1) 36:12=3մ, 2)  3×15=45մ, Պատ.՝ 45մ։ 

Տնային առաջադրանքներ

1․ Ստուգե՛ք հավասարությունը՝ կատարելով բազմապատկումը: (բազմապատկումը կատարի՛ր paint ծրագրում)

• 15∙18=18∙15=270
• 24∙12=12∙24=288
• 21∙44=44∙21=924

2․  Կիրառելով բազմապատկման զուգորդական օրենքը հաշվել առավել հարմար եղանակով:

• 72∙6∙0=0
• 15∙4∙11=660
• 30‧40‧5=30x5x40=6000
• 38‧24‧50=38x50x24=45600

3. Կիրառելով բազմապատկման տեղափոխական և զուգորդական օրենքները հաշվել առավել հարմար եղանակով:

• ●      8∙3∙5=8x5x3=120
• 11∙2∙30∙5= 11∙2x5x30=6600
• 17∙8∙4∙5=5x4x8x17=2720

4. Հաշվե՛ք գումարը՝ գումարումը փոխարինելով բազմապատկումով՝

• 27+27+27+27+27+27+27=27×7=189
• 104+104+104+104+104+104+104 =7×104=728

Բնական թվերի  գումարման տեղափոխական և զուգորդական օրենքները

Գումարվող թվերը կոչվում են գումարելիներ, իսկ գումարման արդյունքը՝ գումար։

Բնական թվերի գումարման տեղափոխական օրենք․

Գումարելիների տեղերը փոխանակելիս գումարը չի փոխվում։ 

Բնական թվերի գումարման զուգորդական օրենքը․

Եթե երկու թվերի գումարին գումարվում է երրորդ թիվը, արդյունքը հավասար կլինի այն թվին, որը ստացվում է, եթե առաջին թվին գումարվում է երկրորդ և երրորդ թվերի գումարը։

Դասարանական առաջադրանքներ․

1․ Գտե՛ք առաջին երեք կարգային միավորների գումարը։111

2․ Գտե՛ք ամենամեծ եռանիշ թվի և ամենափոքր քառանիշ թվի գումարը։1999

3․ Կիրառելով գումարման տեղափոխական օրենքը՝ հաշվել առավել հարմար եղանակով։

• 250+150+200=600
• 796+4+100+250=1150
• 38000+2000+6550=46550

4․ Կիրառելով գումարման զուգորդական օրենքից՝ հաշվեք առավել հարմար եղանակով։

• 13+87+39=139
• 17+283+196=496
• 1032+968+255=2255

5. Կիրառելով գումարման տեղափոխական և զուգորդական օրենքները՝ հաշվեք առավել հարմար եղանակով։

• 64+18+36=64+36+18=118
• 393+8+92+107=393+107+92+8=600
• 2059+2311+441+689+14=2059+441+2311+689+14=5514

6․ Մեքենան առաջին օրն անցել է 115կմ, երկրորդ օրը՝ 15կմ-ով ավելի։ Երրորդ օրը մեքենան անցել է 10կմ-ով ավելի, քան առաջին երկու օրում։ Ընդամենը քանի՞ կիլոմետր է անցել մեքենան երեք օրում։115+15=130  130+10=140   115+140+130=375, Պատ.՝ 375 կմ

7․Հինգ միանման աթոռակներն արժեն 18000 դրամ։ Ինչքա՞ն պետք է վճարել 12 այդպիսի աթոռակների համար։18000:5=3600  3600×12=43200 Պատ.՝ 43200 դրամ։

Տնային առաջադրանքներ․

1․ Գտե՛ք ամենափոքր հնգանիշ թվի և ամենամեծ երկնիշ թվի գումարը։ 10099

2․ Գրե՛ք որևէ երկու եռանիշ թիվ, որոնց գումարը եռանիշ է, և երկու եռանիշ թիվ, որոնց գումարը քառանիշ է։ 101+102=203, 500+510=1010

3․ Կիրառելով գումարման տեղափոխական օրենքը հաշվել առավել հարմար եղանակով։

• 6480+20+500+224 =7224
• 12000+8000+6214=26214
• 7480+20+500=8000

4․ Կիրառելով գումարմ=ան զուգորդական օրենքից՝ հաշվեք առավել հարմար եղանակով։

• 60+40+56=156
• 999+1001+101=2101
• 6667+333+1992=8992

5. Կիրառելով գումարման տեղափոխական և զուգորդական օրենքները՝ հաշվեք առավել հարմար եղանակով։

• 276+24+9+91=400
• 1035+465+101+49=1650
• 654+346+250+750+17=2017

Մեկը և զրոն

Դասարանական առաջադրանքներ․

1․ Երկու թվերից մեկը մյուսով բազմապատկելու և բրան բաժանելու դեպքում ստացվում է նույն 11 թիվը։ Որո՞նք են այդ թվերը։

1

2. Կատարե՛ք գործողությունները․

•  (45:9-24:6) ‧1+2‧1=3
• (1+1):1+1:(3-2)+4‧1-1:1=6
• (25-24) ‧(6-5)+1:1+(8-7) ‧1=3
• (453-452): (17-16)+1‧1=2

3. Առանց գրավոր հաշվուներ կատարելու՝ կռահե՛ք, թե ինչի է հավասար առաջին հինգ կարգային միավորների գումարը։ 11111

4․ Բրուտը 1 օրում պատրաստում էր 5 կճուճ։ Նոր սարք տեղադրելուց հետո նա սկսեց 1 օրում 3 կճուճով ավելի պատրաստել։ Քանի՞ կճուճ կպատրաստի բրուտը 7 օրում։

7×8=56կճուճ,   Պատ.՝ 56կճուճ

Տնային առաջադրանքներ․

1.Կատարե՛ք գործողությունները․

• 5‧1+1։1+3‧1-1‧1=8
• 1:(10-9)+25‧1-1‧14=12
• (1‧38-1‧37):1-1:1=0

2․ Գրե՛ք այն ամենափոքր քառանիշ թիվը, որը չի փոխվում նրա գրառման մեջ թվանշանների ցանկացած տեղափոխության դեպքում։ 1111

3․ Գործածվու՞մ է արդյոք 5 թվանշանը ամենափոքր հնգանիշ թվի գրառման մեջ։ 10000-չի գործածվում

4․ Սկյուռը 10 րոպեում ուտում է 8 ընկույզ։ Քանի՞ րոպեում սկյուռը կուտի 40 ընկույզ։ 50 րոպե

Սեպտեմբերի 22-25

Դասարանական առաջադրանքների փաթեթ

Հաշիվ և թիվ։ Բնական թվեր

Բանավոր հարցեր

1․ Ո՞ր թվերն են կոչվում բնական թվեր։

2․ Ի՞նչ է բնական թվերի շարքը։

3․ Ո՞ր թվով է սկսվում բնական թվերի շարքը։

4․ Բնական թվերի շարքում կա՞ արդյոք մեկին նախորդող թիվ։

5․ Մի՞շտ կարելի է համեմատել երկու բնական թվեր։

6․ Ի՞նչ  նշաններ են գործածվում թվերի համեմատման համար։

Առաջադրանքներ

1․ Թվերը դասավորե՛ք աճման կարգով․ 5, 9, 11, 2, 8, 1, 12, 4, 10, 7, 6, 3

     1,2,3,4,5,6,7,8,9,10,11,12

2․ Ո՞ր թիվն է հաջորդում 19300584 թվին։

    19300585

3․ Ո՞ր թիվն է նախորդում 38657 թվին։

     38656

4․ Համեմատի՛ր․

• 12374 > 9389
• 874563 > 785674
• 567213 > 567211
• 148645 > 48645
• 298467 = 298467
• 478478 < 645470
• 2367894 և 2367994
• 13456 < 53456
• 4789645 > 568129
• 578478 < 649784
• 9784512 = 9784512

5․ Երկու թվերի գումարը 390 է։ Գումարելիներից մեկը հաշվման ժամանակ նախորդում է 10 թվին։ Գտե՛ք մյուս գումարելին։   381

6․ Մի գրքույկում կա 20 էջ, մյուսում՝ 56։ Քանի՞ էջ կա այն գրքում որի էջերի քանակը 7 անգամ ավելի է, քան երկու գրքույկներինը միասին։

20+56=76    76×7=532 էջ,

7․  Գինու երկու կարաս կա։ Առաջինում կար 100լ գինի։ Երբ նրանից վերցրին 30լ գինի, նրա մեջ մնաց երկու անգամ պակաս գինի, քան երկրորդում եղածն էր։ Որքա՞ն գինի կար երկրորդ կարասում։

100-30=70 ,    70×2=140 լ գինի, Պատ.՝ 140 լ գինի։

8․ Երկու կայարանների հեռավորությունը 350կմ է։ Առաջին գնացքն այդ ճանապարհն անցնում է 2 ժամով պակաս ժամանակաում, քան երկրորդը։ 1 ժամում քանի՞ կիլոմետր է անցնում առաջին գնացքը, եթե երկրորդը 1 ժամում անցնում է 50 կմ։

350:50=7        7-2=5   350 :5 =70    Պատ.՝70կմ

9․ Երկու նավամատույցների միջև եղած 120կմ ճանապարհը նավակն անցնում է 6 ժամում։ Եթե նավակը ճանապարհի միջնակետում (ճանապարհի կեսն անցնելուց հետո) սկսի 1ժամում 10կմ-ով ավելի անցնել, քանի՞ ժամում մի նավամատույցից կհասնի մյուսը։

1)120:6=20 , 2) 120:2=60, 3) 60:20=3, 4)20+10=30, 5)60:30=2, 6)2+3=5 Պատ.՝5ժամ 

10․ Գրապահարանի երկու դարակներում կա 102 գիրք։ Եթե առաջին դարակից 12 գիրք հանենք, ապա դարակներում միևնույն քանակով գրքրեր կմնա։ Քանի՞ գիրք կա դարակներից ամեն մեկում։

1)102+12=114      2)114:2=57           57-12=45   Պատ.՝45, 57 գիրք

1․ Հեծյալը առաջին օրը անցավ 62կմ, երկրորդ օրը՝ 15կմ-ով ավելի։ Քանի՞ կիլոմետր անցավ հեծյալը երկու օրում։

62+15+62=139        Պատ.` 139 կմ

2․ Գյուղն ունի 5632 բնակիչ։ Նրանցից 1920-ը տղամարդիկ են, 2053-ը՝ կանայք, մնացածները՝ երեխաներ։ Քանի՞ երեխա է ապրում գյուղում։

1920+2053=3973     5632-3973=1659    Պատ.՝ 1659 երեխա

3. Կարմիր զարդատուփում կա 10 մատանի, կապույտ զարդատուփում՝ 7մատանիով ավելի, իսկ կանաչ զարդատուփու՝ 3 մատանիով ավելի, քան կապույտում։ Ընդամենը քանի՞ մատանի կա երեք զարդատուփերում։

10+17+20=47     Պատ.՝ 47 մատանի  

Տնային առաջադրանքներ

1.Գարնանը այգում տնկեցին 200 ծառ, որոնցից 48-ը նռենիներ էին, մնացածները՝ դեղձենիներ։ Դեղձենու տնկիներից 52-ը չարմատակալեցին։ Այգում քանի՞ դեղձենի ծաղկեց այդ գարնանը։

200-48=152    152-52=100        Պատ.՝ 100 դեղձենի

2. Մի տոպրակում կա 264 ընկույզ, իսկ մյուսում՝ 305։ Առաջին տոպրակից երկրորդ տեղափոխեցին 82 ընկույզ, ապա երկրորդից առաջին՝ 117 ընկույզ։ Քանի՞ ընկույզ եղավ տոպրակներից ամեն մեկում։

117-82=35   264+35=299   305-35=270       Պատ.` 1_299 ընկույզ   2_270 ընկույզ

Տնային առաջադրանքների փաթեթ  

Թվանշաններ։ Թվերի գրառումը

1․ Քանի՞ տարբեր թվանշաններ են գործածվում 848778 թվի գրառման մեջ։ 3

2․ Քանի՞ տարբեր թվանշաններ են գործածվում 1234789 թվի գրառման մեջ։ 7

3․ Քանի՞ թվանշան կգործածվի տասներկու էջանոց գրքույկի էջերը համարակալելու համար 15։ Ո՞ր թվանշանները կգործածվեն մեկից ավելի անգամ։  1, 2

Կարգեր։ Կարգային միավորներ

4․ Քանի՞ կարգ կա հետևյալ թվերից յուրաքանչյուրում․

• 735 – 3 կարգ
• 1096- 4 կարգ
• 30672 -5 կարգ
• 8-1 կարգ

5․ Հետևյալ թվերը ներկայացված են կարգային գումարելիների գումարի տեսքով։ Ինչպիսի՞ն կլինեն դրանց դիրքային գրառումները․

8 ∙1000 +5∙100+6∙1=8506=8506

5∙100000+4∙10000+3∙1000+2∙100+1∙10=543210

6․ Հետևյալ թվերը գրի՛ կարգային գումարելիների գումարի տեսքով․

• 734=7×100+3×10+4×1
• 40550=4×10000+5×100+5×10
• 671000=6×100000+7×10000+1×1000

Դասարանական առաջադրանքների փաթեթ  

Թվանշաններ։ Թվերի գրառումը

Հարցեր

1․ Ի՞նչ է թվանշանը։ Միանիշ թվերն են

2․ Քանի՞ թվանշան է գործածվում թվերի գրառման համար։ 10

3․ Ինչպե՞ս են կոչվում և որտե՞ղ են ստեղծվել այն թվանշանները, որոնք մենք գործածում ենք։ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 թվանշանները կոչվում են արաբական։

4․ Այժմ գործածվող թվանշաններից բացի՝ ուրիշ ի՞նչ թվանշաններ են ձեզ հայտնի։

Հռոմեական թվանշանները։

Առաջադրանքներ

5․ Քանի՞ տարբեր թվանշաններ են գործածվում 8306388 թվի գրառման մեջ։ 4

6․Քանի՞ տարբեր թվանշաններ են գործածվում 14865 թվի գրառման մեջ։5

7․ Քանի՞ տարբեր թվանշաններ են գործածվում 999999 թվի գրառման մեջ։ 1

8․ Չհրկիզվող պահարանը բացելու համար անհրաժեշտ է իմանալ նրա գաղտնագիրը, որը կազմված է երեք տարբեր թվանշաններից։ Գրե՛ք այն բոլոր հնարավոր գաղտնագրերը, որոնք կազմված են 0, 1, 2 թվանշաններից։120, 012 102, 201, 210

9․ Քանի՞ թվանշան կգործածվի տասնհինգ էջանոց գրքույկի էջերը համարակալելու համար 21։ Ո՞ր թվանշանները կգործածվեն մեկից ավելի անգամ։ 1,2,3,4,5,

Կարգեր։ Կարգային միավորներ

10․ Քանի՞ կարգ կա հետևյալ թվերից յուրաքանչյուրում․

• 536 -3
• 25-2
• 7-1
• 8394-4
• 956630-6

11․ Հետևյալ թվերը ներկայացված են կարգային գումարելիների գումարի տեսքով։ Ինչպիսի՞ն կլինեն դրանց դիրքային գրառումները․

7∙10000+6∙1000+4∙100+5∙10+3∙1=76453

8∙10000+3∙100+2∙10+7∙1=80327

12․ Հետևյալ թվերը գրի՛ կարգային գումարելիների գումարի տեսքով․

• 3893=3∙1000+8∙100+9∙10+3∙1
• 45399=4×10000+5×1000+3×100+9×10+9×1
• 300201=3×100000+2×100+1×1
• 80006=8×10000+6×1

Տարբերակ 1

1․ Գտե՛ք թվի բոլոր բաժանարարները.

24  —        1, 2, 3, 4, 6, 8, 12, 24

36  —        1, 2, 3, 4, 6, 9, 12, 18, 36

19-          1, 19 

2․ Թվերը դասավորի՛ր աճման կարգով․

95,654, 3784,3785,7452 ,

3.  Հայտնի է , որ թիվը բաժանվում է  9-ի, ի՞նչ թվանշան  պետք է գրված լինի *-ի փոխարեն:   *110

  7           

4. Արտահայտի՛ր 8կմ6մ5դմ-ը դեցիմետրերով։

80065

5. Բերված օրինակներում աստղանիշները փոխարինել անհրաժեշտ թվանշաններով

ա) 6950-4094=2856

բ)

     27

 X

    35

  135

+81

  945

7. Ուղղանկյան երկարությունը 16 սմ է, իսկ լայնությունը 2 անգամ փոքր է երկարությունից: Գտի՛ր այդ ուղղանկյան մակերեսը:

1. 16:2=8սմ,    2. 16×8=128 սմ

8. Երկու մառաններում 1183 շիշ գինի կա, առաջինում երկրորդից 183-ով ավելի է։ Ամեն մառանում քանի՞ շիշ գինի կա։

   1.1183- 183= 1000   2. 1000:2=500 շիշ 2-րդում    3. 500+183=683  շիշ 1-ինում        

9. Հաշվի՛ր արտահայտության արժեքը․

   (5000-50×5):10-75=400

10․ Մի շարքում կանգնած են Անին, Դավիթը, Սյուզին, Նարեկը և Արենը: Անին գտնվում է Սյուզիից ձախ, բայց Նարեկից աջ: Նարեկն ու Արենը իրար կողք կանգնած չեն, իսկ Դավիթը չի գտնվում ո՛չ Նարեկի կողքը, ո՛չ Արենի կողքը, ո՛չ էլ Անիի կողքը: Ի՞նչ հերթականությամբ են կանգնած նրանք:

Գործնական աշխատանք

Ֆոտոշարքը պարտադիր է, որպեսզի տեսանելի լինի, որ աշխատանքը դուք եք կատարել։ Կարող եք պատրաստել նաև տեսաֆիլմ։

Ընթացքը․

• Ինքնուրույն ուսումնասիրում ես ուղղանկյունանիստ, խորանարդ թեման
• Քեզ կօգնի ուսումնական տեսանյութը
• Գունավոր ստվարաթղթից պատրաստի՛ր խորանարդ
• Քեզ կօգնի ուսումնական տեսանյութը